Piece-wise exponential (Additive Mixed) Modeling Tools

Piece-wise exponential (Additive Mixed) Modeling ToolsISCB41, 2020

Andreas Bender (@adibender), 
 Fabian Scheipl, David Rügamer, Philipp Kopper, Bernd Bischl, Helmut Küchenhoff

Department of Statistics, LMU Munich1

The framework is general in the sense that

it supports different Survival Tasks
- right-censoring, left-truncation
- time-varying effects, time-varying features
- cumulative effects (weighted cumulative exposure, distributed lag models)
- competing risks, multi-state models
does not require specialized Software, can be applied
- across programming languages and
- using any algorithm that supports optimization of the Poisson Likelihood

$\usepackage a m s m a t h, a m s s y m b, b m$

(source: Bender, et al. (2020))

$\usepackage a m s m a t h, a m s s y m b, b m$

Survival Analysis as Poisson Regression

Consider setting with right-censored data:

we observe $(t_{i}, δ_{i}), i = 1, \dots, n$ , where
- $t_{i} = min (T_{i}, C_{i})$ ; $T_{i} \sim F ⊥ C_{i} \sim G; T_{i}, C_{i} > 0$
- $δ_{i} = I (T_{i} \leq C_{i}) \in {0, 1}$

To approximate $λ (t; x_{i}) = \exp (g (x_{i} (t), t)) \overset{P H}{=} λ_{0} (t) \exp (x_{i}^{'} β)$

Consider setting with right-censored data:

we observe $(t_{i}, δ_{i}), i = 1, \dots, n$ , where
- $t_{i} = min (T_{i}, C_{i})$ ; $T_{i} \sim F ⊥ C_{i} \sim G; T_{i}, C_{i} > 0$
- $δ_{i} = I (T_{i} \leq C_{i}) \in {0, 1}$

To approximate $λ (t; x_{i}) = \exp (g (x_{i} (t), t)) \overset{P H}{=} λ_{0} (t) \exp (x_{i}^{'} β)$

split the follow-up in $J$ intervals $(κ_{j - 1}, κ_{j}], j = 1, \dots, J$

Consider setting with right-censored data:

we observe $(t_{i}, δ_{i}), i = 1, \dots, n$ , where
- $t_{i} = min (T_{i}, C_{i})$ ; $T_{i} \sim F ⊥ C_{i} \sim G; T_{i}, C_{i} > 0$
- $δ_{i} = I (T_{i} \leq C_{i}) \in {0, 1}$

To approximate $λ (t; x_{i}) = \exp (g (x_{i} (t), t)) \overset{P H}{=} λ_{0} (t) \exp (x_{i}^{'} β)$

split the follow-up in $J$ intervals $(κ_{j - 1}, κ_{j}], j = 1, \dots, J$
assume piece-wise constant hazards: $\begin{aligned} λ (t | x_{i} (t)) & \equiv \exp (g (x_{i j}, t_{j})) := λ_{i j}, \forall t \in (κ_{j - 1}, κ_{j}], \end{aligned}$

Consider setting with right-censored data:

we observe $(t_{i}, δ_{i}), i = 1, \dots, n$ , where
- $t_{i} = min (T_{i}, C_{i})$ ; $T_{i} \sim F ⊥ C_{i} \sim G; T_{i}, C_{i} > 0$
- $δ_{i} = I (T_{i} \leq C_{i}) \in {0, 1}$

To approximate $λ (t; x_{i}) = \exp (g (x_{i} (t), t)) \overset{P H}{=} λ_{0} (t) \exp (x_{i}^{'} β)$

split the follow-up in $J$ intervals $(κ_{j - 1}, κ_{j}], j = 1, \dots, J$
assume piece-wise constant hazards: $\begin{aligned} λ (t | x_{i} (t)) & \equiv \exp (g (x_{i j}, t_{j})) := λ_{i j}, \forall t \in (κ_{j - 1}, κ_{j}], \end{aligned}$

Estimation using
- Piece-wise Exponential Model (PEM; e.g.: Laird, et al. (1981); Friedman (1982); Carstensen, et al. (2011))
- Piece-wise exponential Additive Mixed Models (PAMM, e.g.: Cai, et al. (2002); Kauermann (2005); Argyropoulos, et al. (2015); Bender, et al. (2018))

Data in "standard" time-to-event format

Data in PED format

$\to$ transform to PED using $κ_{0} = 0, κ_{1} = 1, κ_{2} = 1.5, κ_{3} = 3$

Data in "standard" time-to-event format

Data in PED format

$\to$ transform to PED using $κ_{0} = 0, κ_{1} = 1, κ_{2} = 1.5, κ_{3} = 3$

Data in "standard" time-to-event format

Data in PED format

$\to$ transform to PED using $κ_{0} = 0, κ_{1} = 1, κ_{2} = 1.5, κ_{3} = 3$

define: $δ_{i j} = {\begin{cases} 1 & t_{i} \in (κ_{j - 1}, κ_{j}] \land δ_{i} = 1 \\ 0 & else \end{cases}$

Data in "standard" time-to-event format

Data in PED format

$\to$ transform to PED using $κ_{0} = 0, κ_{1} = 1, κ_{2} = 1.5, κ_{3} = 3$

define: $δ_{i j} = {\begin{cases} 1 & t_{i} \in (κ_{j - 1}, κ_{j}] \land δ_{i} = 1 \\ 0 & else \end{cases}$ , $t_{i j} = {\begin{cases} t_{i} - κ_{j - 1} & δ_{i j} = 1 \\ κ_{j} - κ_{j - 1} & else \end{cases}$

Data in "standard" time-to-event format

Data in PED format

$\to$ transform to PED using $κ_{0} = 0, κ_{1} = 1, κ_{2} = 1.5, κ_{3} = 3$

define: $δ_{i j} = {\begin{cases} 1 & t_{i} \in (κ_{j - 1}, κ_{j}] \land δ_{i} = 1 \\ 0 & else \end{cases}$ , $t_{i j} = {\begin{cases} t_{i} - κ_{j - 1} & δ_{i j} = 1 \\ κ_{j} - κ_{j - 1} & else \end{cases}$ , $t_{j} := κ_{j}$

Data in "standard" time-to-event format

Data in PED format

$\to$ transform to PED using $κ_{0} = 0, κ_{1} = 1, κ_{2} = 1.5, κ_{3} = 3$

define: $δ_{i j} = {\begin{cases} 1 & t_{i} \in (κ_{j - 1}, κ_{j}] \land δ_{i} = 1 \\ 0 & else \end{cases}$ , $t_{i j} = {\begin{cases} t_{i} - κ_{j - 1} & δ_{i j} = 1 \\ κ_{j} - κ_{j - 1} & else \end{cases}$ , $t_{j} := κ_{j}$

General log-likelihood contribution:

$\begin{aligned} ℓ_{i} & = \log (λ (t_{i}; x_{i})^{δ_{i}} S (t_{i}; x_{i})) \\ = \sum_{j = 1}^{J_{i}} (δ_{i j} \log λ_{i j} - λ_{i j} t_{i j}) \end{aligned}$

Working Assumption $δ_{i j} \overset{i i d}{\sim} P o (μ_{i j} = λ_{i j} t_{i j})$ :

$\begin{aligned} ℓ_{i} & = \log (\prod_{j = 1}^{J_{i}} f (δ_{i j})) \\ = \sum_{j = 1}^{J_{i}} δ_{i j} \log (λ_{i j}) + δ_{i j} \log (t_{i j}) - λ_{i j} t_{i j} \end{aligned}$

Competing risks setting with event types $k \in {1, 2}$

Data in "standard" format

Data in PED format

$\to$ transform to PED using $κ_{0} = 0, κ_{1} = 1, κ_{2} = 1.5, κ_{3} = 3$

$\to$ estimate $λ (t | x, k) = \exp (f (x (t), t, k)), k \in {1, 2}$

Competing risks setting with event types $k \in {1, 2}$

Data in "standard" format

Data in PED format

$\to$ transform to PED using $κ_{0} = 0, κ_{1} = 1, κ_{2} = 1.5, κ_{3} = 3$

$\to$ estimate $λ (t | x, k) = \exp (f (x (t_{j}), t_{j}, k)), \forall t \in (κ_{j - 1}, κ_{j}], k \in {1, 2}$

PEM/GLM: $λ (t) = λ_{0 j} = \exp (β_{0 j}), \forall t \in (κ_{j - 1}, κ_{j}], j = 1, \dots, J$

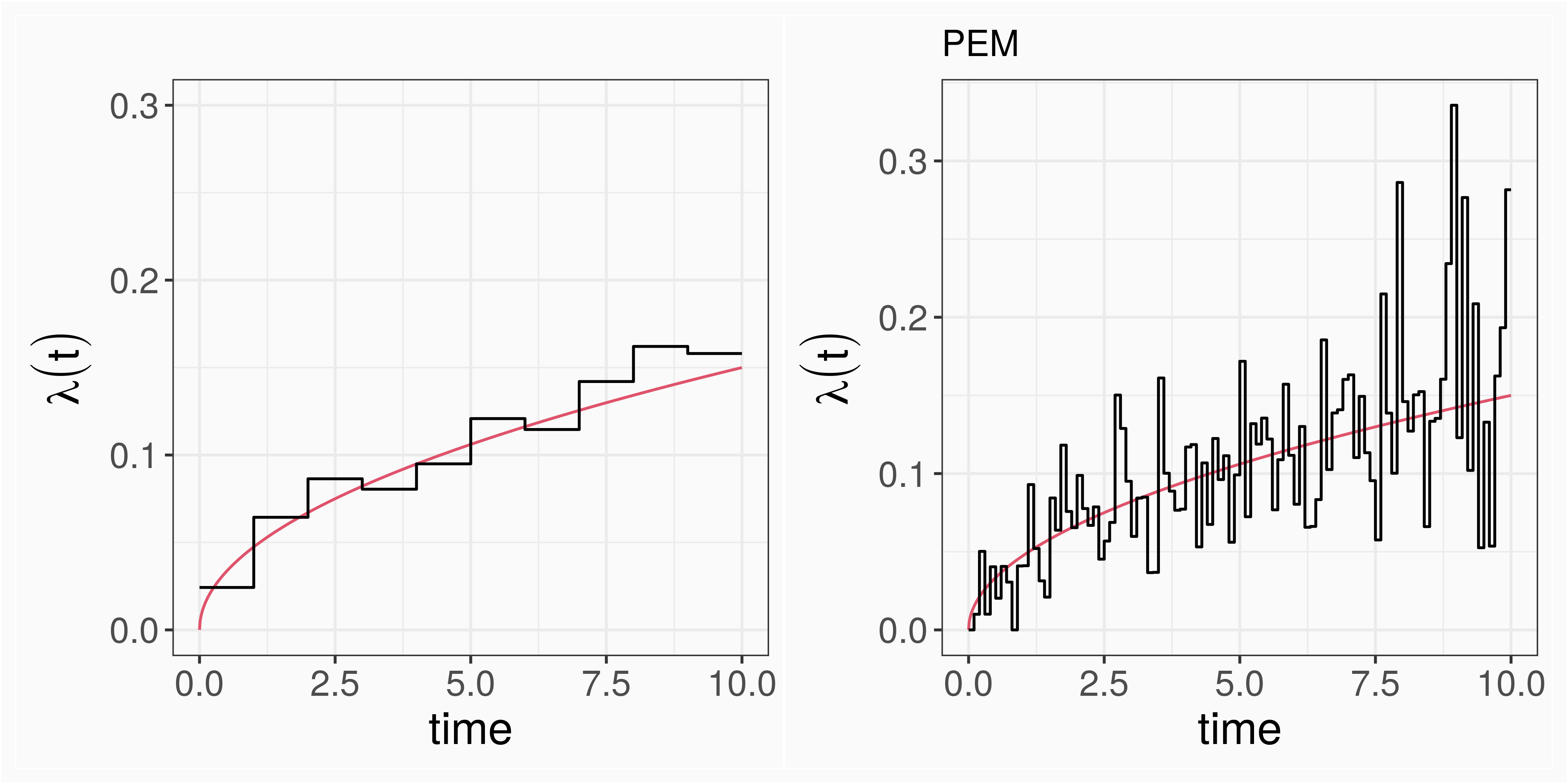
trade of w.r.t. to number of split points (less flexible/more robust vs. more flexible/less robust)
computationally inefficient (one parameter for each interval), especially when considering time-varying effects
results sensitive to number and placement of interval cut points

PAMM/GAMM: $λ (t) = λ_{0 j} = \exp (f_{0} (t_{j})), \forall t \in (κ_{j - 1}, κ_{j}], j = 1, \dots, J; f_{0} (t_{j}) = \sum_{q = 1}^{Q} β_{0 q} B_{0 q} (t_{j})$

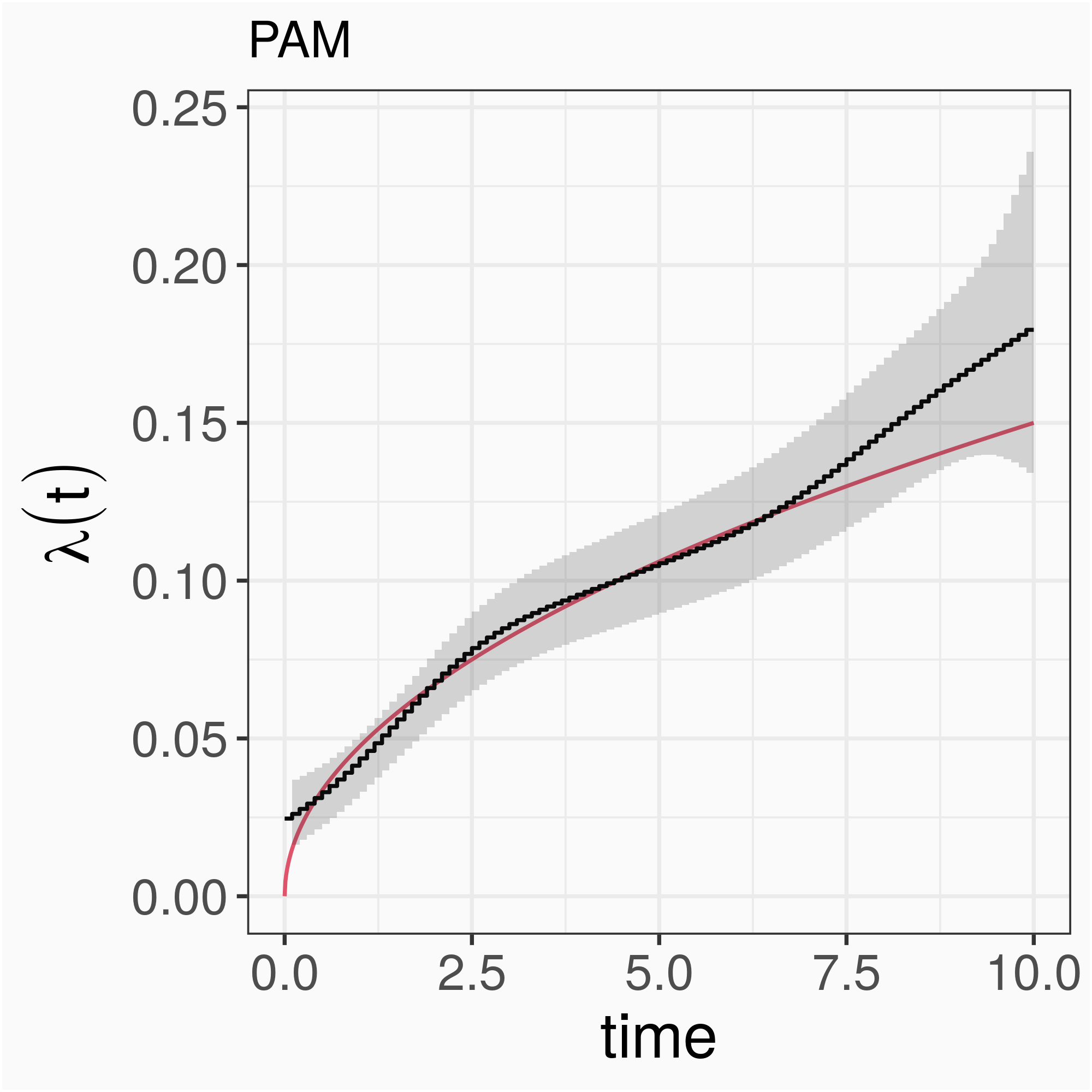
large differences between neighboring coefficients/baseline hazards of neighboring intervals are penalized
insensitive to number and placement of split points
number of parameters to estimate determined by basis dimension $Q$ , not number of intervals $J$

Time-varying effects

In the PEM/PAMM framework, time-varying effects are simply interactions of time $t_{j}$ and other covariates.
$\log (λ (t | x)) = f_{01} (t_{j}) I (c o m p l i c a t i o n s = y e s) + f_{02} (t_{j}) I (c o m p l i c a t i o n s = n o)$

pam_tumor <- mgcv::gam(formula=ped_status~s(tend, by=complications), data=ped_tumor, family=poisson(), offset=offset)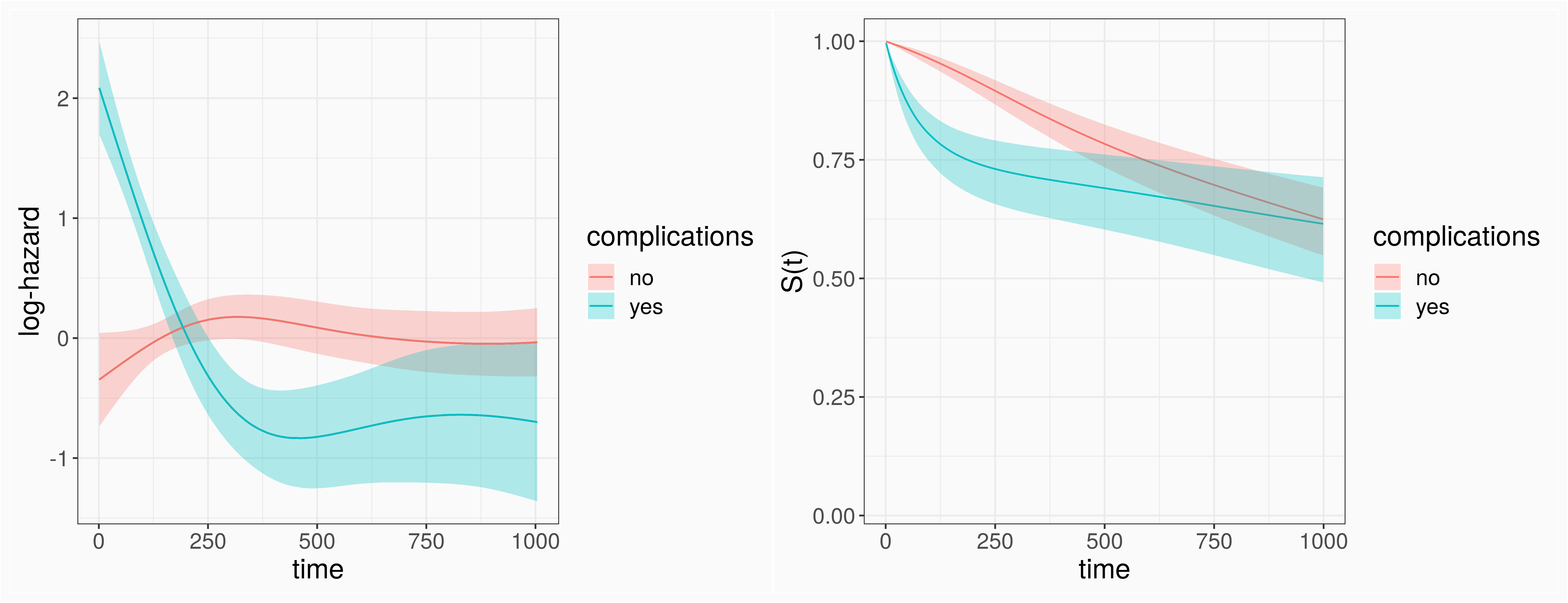

# "Regular" GAM
mgcv::gam(formula=ped_status~s(tend, by=complications), data=ped_tumor, family=poisson(), offset=offset)
# GAM with monotinicity constraints
scam::scam(formula=ped_status~s(tend, by=complications, bs = "mpd"), data=ped_tumor, family=poisson(), offset=offset)
# Bayesian GAM
brms::brm(formula=ped_status~s(tend, by=complications) + offset(offset), data=ped_tumor, family=poisson())

Competing Risks

$\log (λ (t | x)) = f_{01} (t_{j}) I (k = 1) + f_{01} (t_{j}) I (k = 2)$ Cause specific hazards are time-varying effects of time $t_{j}$ and covariate "event type" $k$

pam_cr <- mgcv::gam(formula = ped_status ~ s(tend, by = cause), data = ped_stacked, family = poisson(), offset = offset)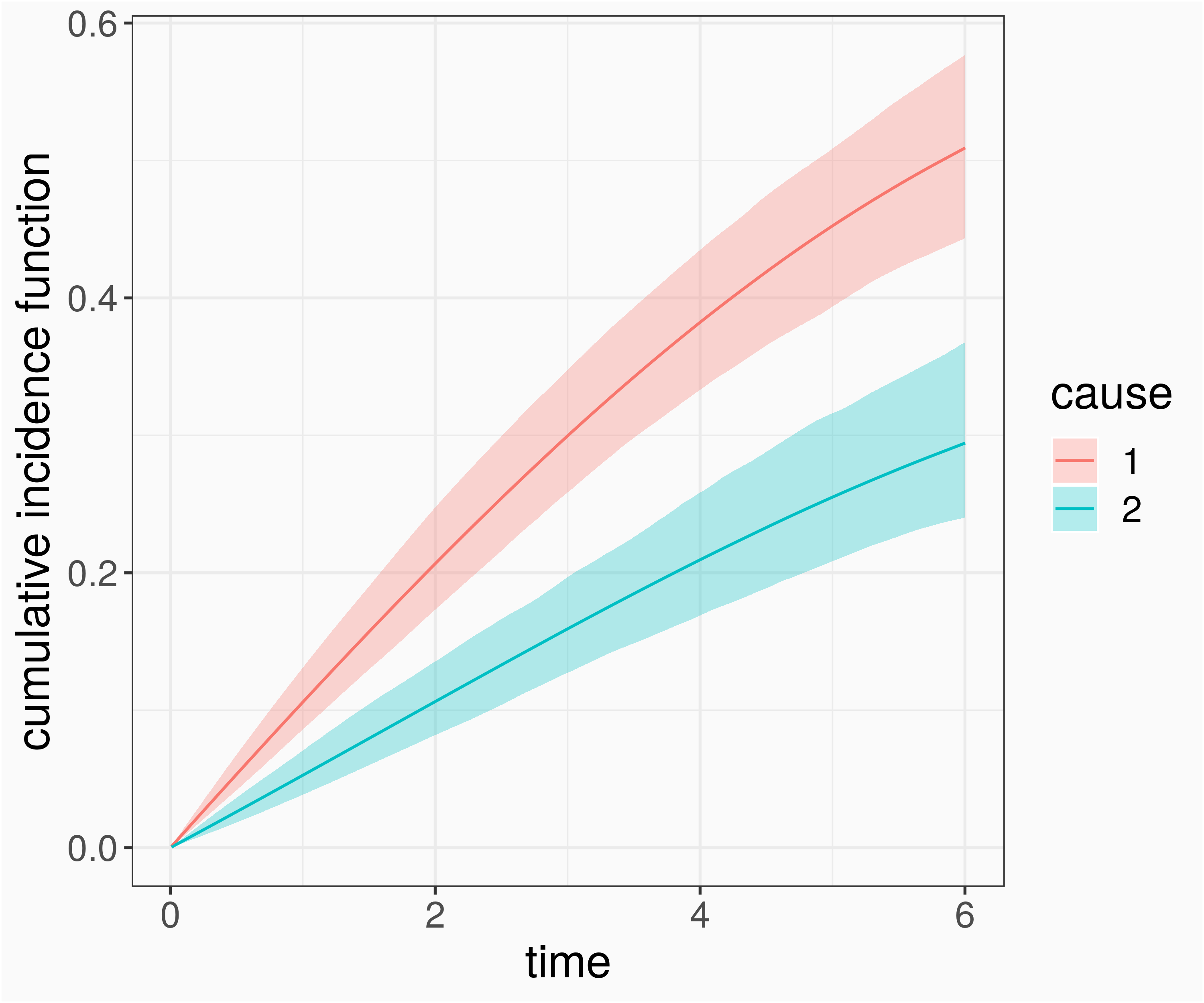

Tree based methods

Time-varying effects Shared vs. cause-specific effects (in CR)

(source: Bender, et al. (2020))

The pammtools package

PEMs/PAMMs powerfull framework for survival analysis, but cumbersome to work with

pammtools facilitates

data transformation (as_ped):
- right-censoring
- cumulative effects
- competing risks
post-processing:
- prediction (add_hazard, add_surv_prob, add_cif),
- model evaluation (integrated brier score via pec)
convenience functions for visualisation, ...

Outlook

support for multi-state models
facilitate extensions: S3 functions for calculation of hazard for other packages (e.g. mbooost, brms)
Prototype for PEMs using xgboost available: https://github.com/adibender/pem.xgb
However, ML algorithms need a different infrastructure (resampling, tuning, benchmarking)
$\to$ Development will probably continue in mlr3 and mlr3proba (Lang, et al. (2019); Sonabend, et al. (2020))

References

Argyropoulos, C. et al. (2015). "Analysis of Time to Event Outcomes in Randomized Controlled Trials by Generalized Additive Models". In: PLoS ONE 10.4, p. e0123784. DOI: 10.1371/journal.pone.0123784. URL: http://dx.doi.org/10.1371/journal.pone.0123784.

Bender, A. et al. (2018). "A generalized additive model approach to time-to-event analysis". En. In: Statistical Modelling 18.3-4, pp. 299-321. ISSN: 1471-082X. DOI: 10.1177/1471082X17748083.

Bender, A. et al. (2020). "A General Machine Learning Framework for Survival Analysis". In: arXiv:2006.15442 [cs, stat]. arXiv: 2006.15442.

Cai, T. et al. (2002). "Mixed Model-Based Hazard Estimation". In: Journal of Computational and Graphical Statistics 11.4, pp. 784-798. ISSN: 1061-8600. DOI: 10.1198/106186002862. URL: http://dx.doi.org/10.1198/106186002862.

Carstensen, B. et al. (2011). "Using Lexis Objects for Multi-State Models in R". En. In: Journal of Statistical Software 38.1. Number: 1, pp. 1-18. ISSN: 1548-7660. DOI: 10.18637/jss.v038.i06. URL: https://www.jstatsoft.org/index.php/jss/article/view/v038i06.

Friedman, M. (1982). "Piecewise Exponential Models for Survival Data with Covariates". In: The Annals of Statistics 10.1, pp. 101-113. ISSN: 00905364. URL: http://www.jstor.org/stable/2240502.

References

Kauermann, G. (2005). "Penalized spline smoothing in multivariable survival models with varying coefficients". In: Computational Statistics & Data Analysis 49.1, pp. 169-186. ISSN: 0167-9473. DOI: 10.1016/j.csda.2004.05.006. URL: http://www.sciencedirect.com/science/article/pii/S0167947304001240.

Laird, N. et al. (1981). "Covariance Analysis of Censored Survival Data Using Log-Linear Analysis Techniques". In: Journal of the American Statistical Association 76.374, pp. 231-240. DOI: 10.2307/2287816. URL: http://www.jstor.org/stable/2287816.

Lang, M. et al. (2019). "mlr3: A modern object-oriented machine learning framework in R". In: Journal of Open Source Software. DOI: 10.21105/joss.01903. URL: https://joss.theoj.org/papers/10.21105/joss.01903.

Sonabend, R. et al. (2020). "mlr3proba: Machine Learning Survival Analysis in R". In: arXiv:2008.08080 [cs, stat]. arXiv: 2008.08080. URL: http://arxiv.org/abs/2008.08080 (visited on Aug. 20, 2020).

↑, ←, Pg Up, k	Go to previous slide
↓, →, Pg Dn, Space, j	Go to next slide
Home	Go to first slide
End	Go to last slide
Number + Return	Go to specific slide
b / m / f	Toggle blackout / mirrored / fullscreen mode
c	Clone slideshow
p	Toggle presenter mode
t	Restart the presentation timer
?, h	Toggle this help

Piece-wise exponential (Additive Mixed) Modeling Tools

ISCB41, 2020

Andreas Bender (),
Fabian Scheipl, David Rügamer, Philipp Kopper, Bernd Bischl, Helmut Küchenhoff

Department of Statistics, LMU Munich

The framework is general in the sense that

Time-varying effects

Competing Risks

Tree based methods

Outlook

References

References

The framework is general in the sense that

Help

Piece-wise exponential (Additive Mixed) Modeling Tools

ISCB41, 2020

Andreas Bender (@adibender), Fabian Scheipl, David Rügamer, Philipp Kopper, Bernd Bischl, Helmut Küchenhoff

Department of Statistics, LMU Munich

The framework is general in the sense that

Time-varying effects

Competing Risks

Tree based methods

Outlook

References

References

The framework is general in the sense that

Help

Andreas Bender (),
Fabian Scheipl, David Rügamer, Philipp Kopper, Bernd Bischl, Helmut Küchenhoff