Penalized Estimation of Cumulative Effects

class: center, middle, inverse, title-slide

# Penalized Estimation of Cumulative Effects
### Andreas Bender, F Scheipl, W Hartl, A G Day, H Küchenhoff
### Departement of Statistics, LMU Munich
### 2017/12/17

---

# Outline
<link rel="stylesheet" href="//cdnjs.cloudflare.com/ajax/libs/highlight.js/9.9.0/styles/github.min.css">
<link rel="stylesheet" href="https://cdnjs.cloudflare.com/ajax/libs/font-awesome/4.7.0/css/font-awesome.min.css" integrity="sha512-SfTiTlX6kk+qitfevl/7LibUOeJWlt9rbyDn92a1DqWOw9vWG2MFoays0sgObmWazO5BQPiFucnnEAjpAB+/Sw==" crossorigin="anonymous">

.font150[
- Motivation

- Exposure-Lag-Response Associations

- Application
]

???
`$$\newcommand{\ra}{\rightarrow}
\newcommand{\bs}[1]{\boldsymbol{#1}}
\newcommand{\tn}[1]{\textnormal{#1}}
\newcommand{\mbf}[1]{\mathbf{#1}}
\newcommand{\nn}{\nonumber}
\newcommand{\ub}{\underbrace}
\newcommand{\tbf}[1]{\textbf{#1}}
\newcommand{\E}{\mathbb{E}}
\newcommand{\bfx}{\mathbf{x}}
\newcommand{\bfX}{\mathbf{X}}
\newcommand{\bff}{\mathbf{f}}
\newcommand{\bsbeta}{\boldsymbol{\beta}}
\newcommand{\bsgamma}{\boldsymbol{\gamma}}
\newcommand{\bslambda}{\boldsymbol{\lambda}}
\newcommand{\bfS}{\mathbf{S}}
\newcommand{\bfz}{\mathbf{z}}
\newcommand{\bfZ}{\mathbf{Z}}
\newcommand{\te}{t_e}
\newcommand{\tlag}{t_{\text{lag}}}
\newcommand{\tlead}{t_{\text{lead}}}
\newcommand{\tw}{\mathcal{T}_e(t)}
\newcommand{\Tw}[1]{\mathcal{T}^{#1}}
\newcommand{\tilt}{\tilde{t}}
\newcommand{\Zi}{\mathcal{Z}_i(t)}
\newcommand{\CI}{C1}
\newcommand{\CII}{C2}
\newcommand{\CIII}{C3}
\newcommand{\gCII}{g_{_{\CII}}}
\newcommand{\gCIII}{g_{_{\CIII}}}
\newcommand{\gammaEst}{\hat{\gamma}_g^r}
\newcommand{\hatEj}{\hat{e}_{j, r}}
\newcommand{\diag}{\operatorname{diag}}
\newcommand{\rpexp}{\operatorname{rpexp}}
\newcommand{\Rlang}{\textbf{\textsf{R}}}
\newcommand{\code}[1]{{\small \texttt{#1}}}$$`

---
# Motivation
  - Multi-center study of critical care patients from 457 ICUs
  ( `$\approx 10k$` patients)

- maximum follow up of 60 days
  (we only consider short term survival `$t\leq 30$`)

- Various confounders:
    - Age, Gender, BMI
    - Diagnosis, Admission Category
    - year of ICU admission
    - Apache II Score
    - ICU random effect

- **11-day nutrition protocol**
    - prescribed calories (determined at baseline `$t=0$`)
    - *daily* caloric intake
    - daily **caloric adequacy (CA)** = caloric intake/prescribed calories

---
# Caloric Intake
<img src="image/nutri-hist.jpg">

---
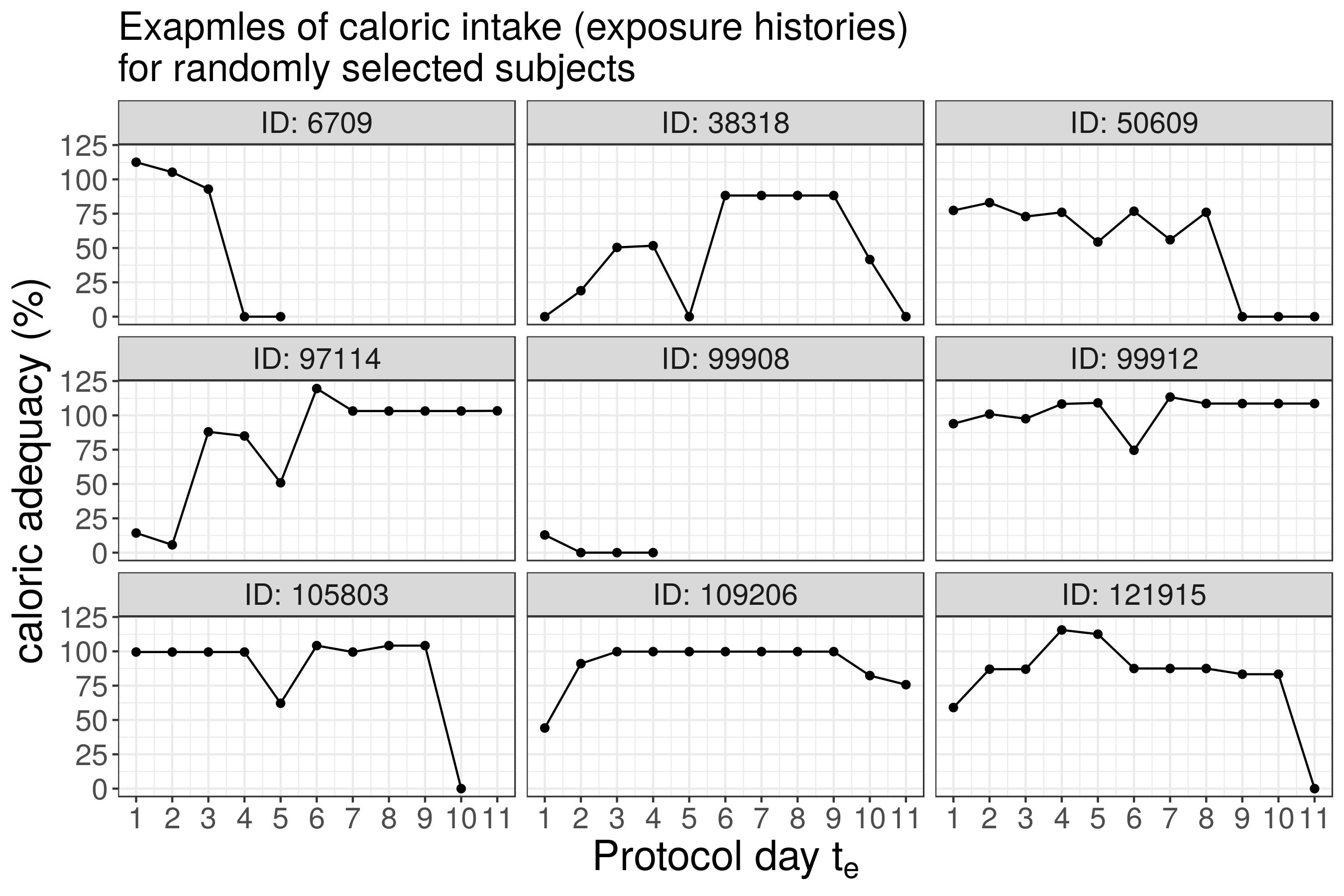
# Motivation
- We are interested in how artificial nutrition (*exposure*) affects short
term survival (*outcome*)

- Difficulty:
  - effect of nutrition might have a temporal delay
  (e.g. nutrition today affects survival 4 days later)

- effect of nutrition might "wear off" after some time
  (e.g. nutrition on day 1 likely won't affect the hazard on day 30)

- the (delayed) effect of nutrition also depends on the amount of nutrition
  (caloric adequacy) provided, possibly non-linearly

- the same amount of exposure might have a different effect depending on
  the follow up and exposure time

- the effect may be *cumulative* (i.e., 5 days of malnutrition in a row may
  be worse than only 2 in a row or 5 days malnutrition scattered throughout the
  follow up while on the other days "correct" amount was provided)

---
# Terminology
We use the following terminology and notation:

- **Time-to-event `$t$`**: Time at which event times are observed

- **Time of exposure `$\te$`**: Time at which values of the exposure are observed
(must not necessarily overlap temporally with `$t$`, measured in the same units
or be in the same domain as `$t$`, e.g. calendar days ( `$\te$`) vs. 24h periods
(days) since admission to ICU `$t$`)

- **time-varying *effects* (TVE)**: Effects of time-constant covariates (covariates
observed at the beginning of the follow-up) that can vary over time `$t$`

- **time-dependent *covariates* (TDC)**: Covariates whose values change over time.
Value changes are recorded at exposure time `$\te$` (here synonymous to *exposure*)

- **Exposure value `$z(\te)$`**: The value of the TDC observed at exposure time
`$\te$`

- **Exposure history `$\mathbf{z}$`**: The complete history of observed
values of the exposure/TDC `$\mathbf{z}= (z(t_{e,1}), z(t_{e,2}), ..., z(t_ {e,Q}))$`

---
# Terminology
**A general cumulative effect/Exposure-Lag-Response Association (ELRA)** can be defined as

.font110[
`$$g(\mathbf{z}, t) = \int_{\te: \te \leq t}h(t, \te, z(\te))\mathrm{d}\te$$`
]
- **Partial effects `$h(t,\te,z(\te))$`**: The effect of the TDC recorded at
exposure time `$\te$` with value `$z(\te)$` on the hazard at follow up time `$t$`
(the tri-variate function `$h$` is potentially non-linear in all three dimensions)

- **Cumulative effect `$g(\mathbf{z}, t)$`**: The total (cumulated) effect of the
partial effects on the log-hazard at time `$t$` given exposure history `$\bfz$`

---
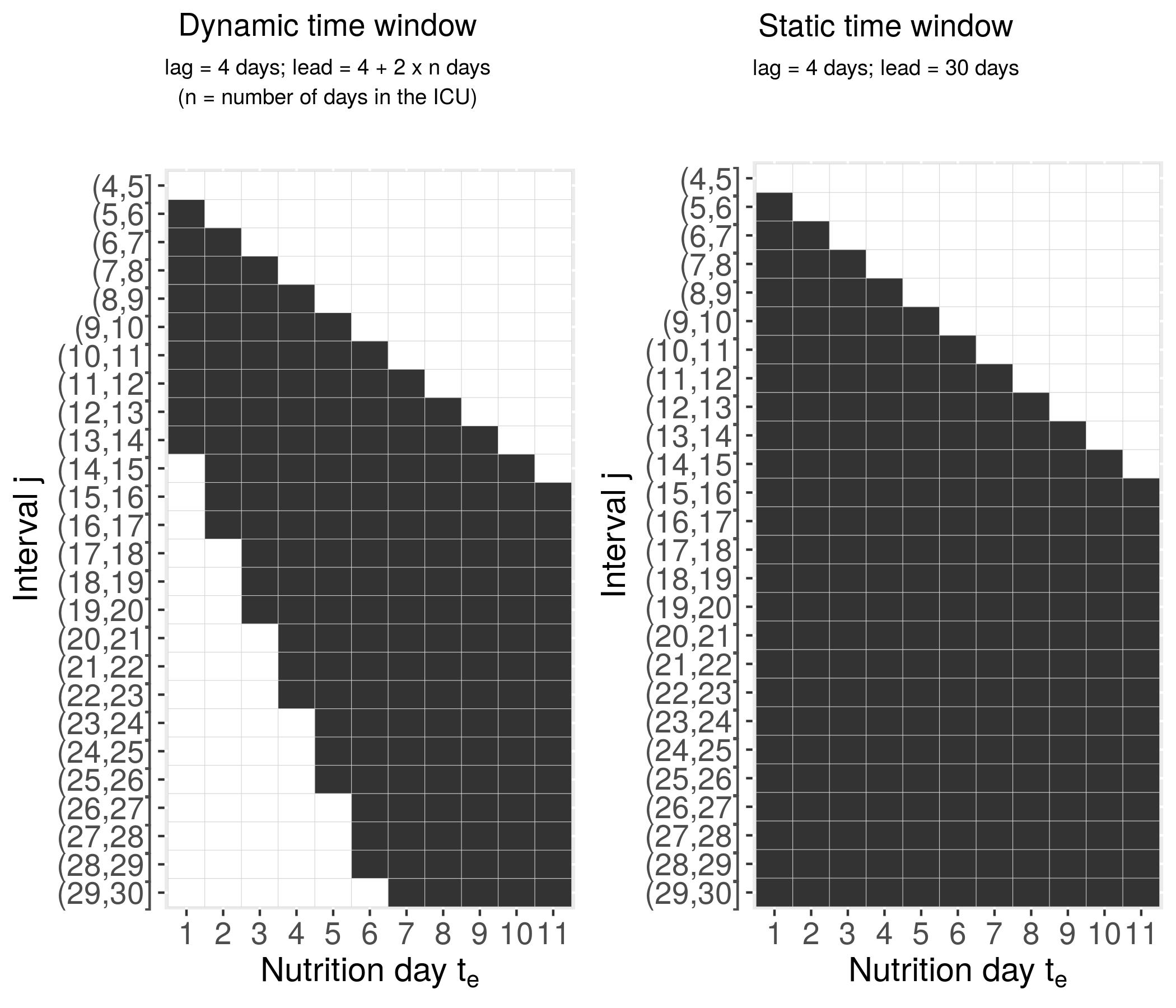
# Lag-Lead-Window
The integration borders can be defined *more* general, such that
`$$g(\mathbf{z}, t) = \int_{t-\tlag - \tlead}^{t-\tlag}h(t, \te, z(\te)) \mathrm{d}\te$$`
- **Lag time `$\tlag$`**: The length of the delay until the TDC recorded at
exposure time `$\te$` starts to affect the hazard (often `$\tlag=0$`)
- **Lead time `$\tlead$`**: The duration of the effect of the TDC observed at exposure time `$\te$`
- `$\tlag$` and `$\tlead$` define the set of exposures that contribute to the
cumulative effect at time `$t$` as `$\{z(\te): \te \in [t-\tlag - \tlead, t-\tlag]\}$`
- Minimal requirement: `$\int_{\te:\te\leq t}$`
- Special case `$\int_0^t$` follows with `$\tlag=0$` and `$\tlead=t$`
- Example ( `$\tlag = 4$`, `$\tlead = 3$`):
  - The last nutrition that will enter the cumulative effect at
  time `$t=10$` is nutrition at `$\te \leq t - \tlag = 10-4=6$`, i.e. `$z(t_{e}=6)$`
  - The earliest nutrition that will contribute to the cumulative effect at time
  `$t=10$` is nutrition at `$\te \geq t - \tlag - \tlead = 10 - 4 - 3 = 3$`

---
# Lag-Lead-Window
The integration borders can be defined *even more* general, such that
.font120[
`$$g(\mathbf{z}, t) = \int_{t-\tlag(\te) - \tlead(\te)}^{t-\tlag(\te)}h(t, \te, z
(\te)) \mathrm{d}\te=\int_{\tw}h(t, \te, z(\te)) \mathrm{d}\te$$`
]

- `$\tlag$` and `$\tlead$` times can themselves depend on (exposure) time

- `$\tw$` is the set of exposure times `$\te$` relevant to the cumulative effect
at time `$t$`

- We call `$\tw$` the *Lag-Lead-Window* or *Window of effectiveness*

---
# Lag-Lead Window (Example)

---
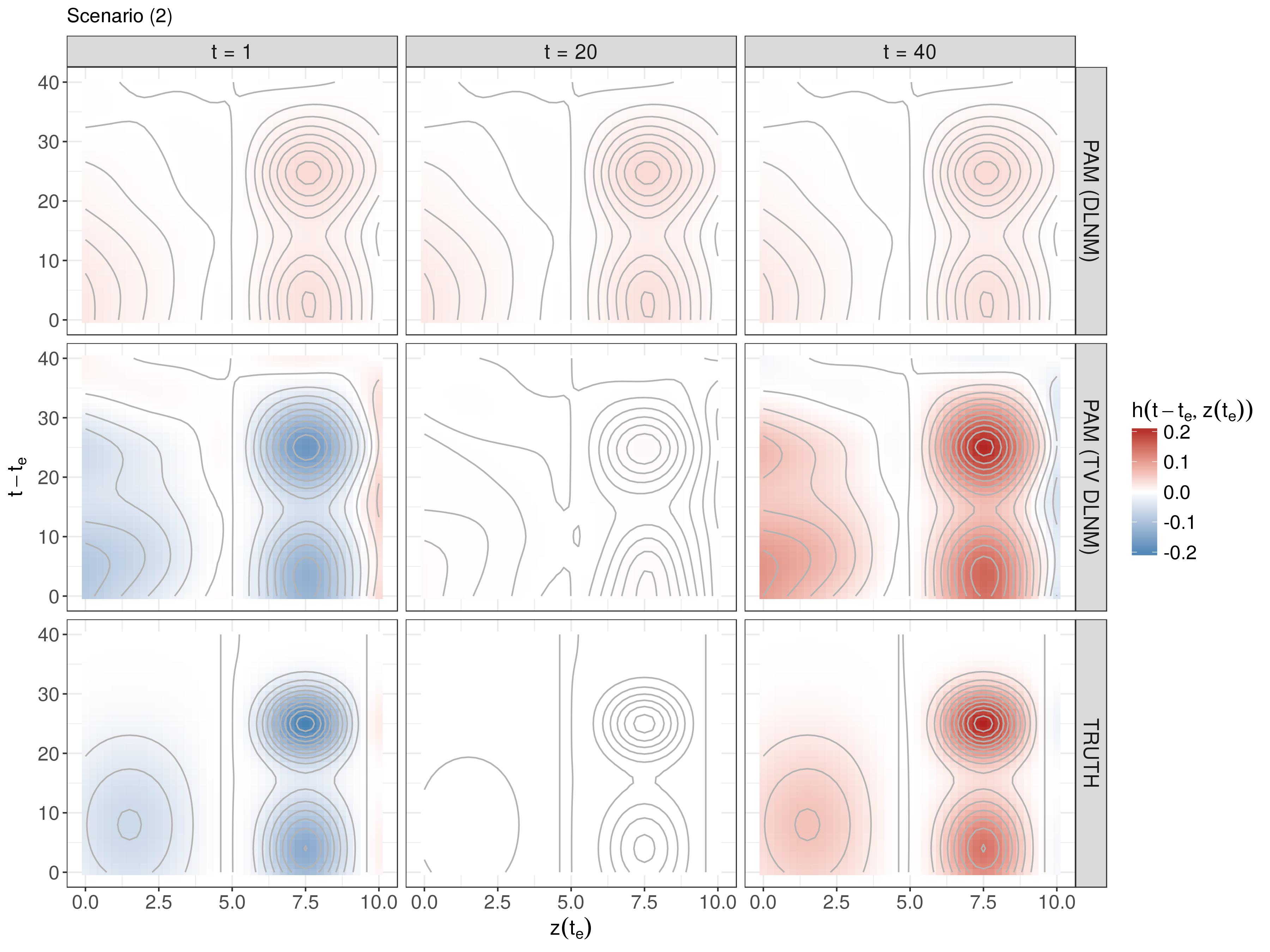
# ELRAs in the literature
Some models known from the literature follow as special cases of the general
specification
`$$g(\mathbf{z}, t) = \int_{\mathcal{T}_e(t)}h(t, t_e, z(t_e))$$`
when we assume that partial effects `$h$` only depend on *latency* `$t-\te$`
instead of concrete combination of `$t$` and `$\te$`, i.e.,
`$h(t=30, \te=3, z(\te))\stackrel{!}{=}h(t=40,\te=13, z(\te))\stackrel{!}{=}\tilde{h} (t-\te=27, z(\te))$`
- DLNM: Distributed Lag Non-linear Models (Gasparrini et al,
[2014](http://onlinelibrary.wiley.com/doi/10.1002/sim.5963/abstract),
[2017](http://onlinelibrary.wiley.com/doi/10.1111/biom.12645/abstract)):
`$g(\mathbf{z}, t) = \int_{\mathcal{T}_e(t)}h(t - t_e, z(t_e))$`

- WCE: Weighted Cumulative Exposure ([Sylvestre and Abrahamowicz, 2009](http://onlinelibrary.wiley.com/doi/10.1002/sim.3701/abstract)):
`$g(\mathbf{z}, t) = \int_{\mathcal{T}_e(t)}h(t - t_e)z(t_e)$`

- Also possible within general framework:
  - more flexible WCE:
  `$g(\mathbf{z}, t) = \int_{\mathcal{T}_e(t)}h(t, t_e)z(t_e)$`
  - time-varying DLNM (TV DLNM):
  `$g(\mathbf{z}, t) = \int_{\mathcal{T}_e(t)}h (t, t - t_e, z(t_e))$`

---
# Exposure-Lag-Response Association
- `$g(\bfz, t)$` represents the cumulative, time-varying effect of
exposure history `$\bfz$` on the log-hazard at time `$t$`

- we define its contribution to the model's additive predictor as

`\begin{align}
g(\bfz_i, t) = \int_{\tw} h(\tilde t_j, \te, z_i(\te)) \mathrm{d}\te
  \approx
    \sum_{q: t_{e,q} \in \tw} \Delta_{q}
      h(\tilde t_j, t_{e,q}, z_i(t_{e,q}))
        \quad\forall\, t \in (\kappa_{j-1}, \kappa_j],
\end{align}`

with
  - `$\tilde{t}_j:= (\kappa_j - \kappa_{j-1})/2, j=1,\ldots, J$`
  - partial effects `$h(\tilde t_j, \te, z_i(\te))$`
  - quadrature weights `$\Delta_{q} = t_{e,q} - t_{e,q-1}$` for numerical integration are given by the time between two consecutive exposure measurements

---
# Tensor product smooths
Low rank representation of the tri-variate smooth function
`$$h(t, \te, z(\te)) = \sum_{\ell=1}^L\sum_{r=1}^R\sum_{m=1}^M
\gamma_{\ell r m}B_m(z(\te))B_r(\te)B_\ell(t)$$`

with
  - model matrix `$\bfX = \bfX_{t}\odot \bfX_{\te} \odot \bfX_{z(\te)}$` and

- penalty `$S = \nu_{z(\te)}\mbf{I}_{d_{R}}\otimes\mbf{I}_{d_L}\otimes\mbf{S}_{z(\te)} + \nu_{\te}\mbf {I}_{d_L}\otimes \mbf{S}_{\te}\otimes\mbf{I}_{d_M} + \nu_{t}\mbf{S}_{t}\otimes\mbf{I}_ {d_R}\otimes\mbf{I}_{d_M}$`

`$\ra$` Estimate parameters `$\bsgamma$` by optimizing
`$D(\bsgamma) + \sum_{k}\nu_k\bsgamma'\mbf{S}_k \bsgamma$` (Wood, 2011), where
- `$D(\bsgamma)$` is the model deviance (of the Poisson GAMM)
- `$\bsgamma$` contains all Spline basis coefficients and random effects
- `$\nu_k$` and `$S_k, k=1,\ldots,K$` are the smoothing parameters and penalty
matrices for the `$k$`-th smooth term, respectively

---
# Exposure-Lag Response Association
- If we restrict the ELRA to be linear in the exposure, i.e.,
`$h(z_i(\te), \te, t) = \tilde h(\te, t)\cdot z_i(\te)$` we can simplify to
`$$g(\bfz_i, t) \approx \sum^Q_{q=1} \tilde\Delta_{i,q} \tilde h(t_{e,q}, t)$$`
with
`$$\tilde\Delta_{i,q} = \begin{cases}
  z_i(t_{e,q})\Delta_{q} & \text{ if } t_{e,q} \in \tw\\ 0
  & \text{ else} \end{cases}$$`

---
# Exposure-Lag Response Association
- Spline bases for the bivariate functions `$\tilde h(\te, t)$` are set up
via tensor product B-spline basis with marginal bases
`$B_{m}(\te), m=1,\dots,M$` and `$B_{k}(t), k=1,\dots,K$` defined over the exposure and
hazard time domains, respectively

- `$M$` and `$K$` delimit the maximal complexity of the ELRA

- `$\tilde h(\te, t) =  \sum_{m=1}^{M}\sum_{k=1}^{K} \gamma_{m,k}B_{m}(\te)B_{k}(t)$`

- Combining above equations yields:
`\begin{align}
g(\bfz_i, t) \approx \sum_{m=1}^{M}\sum_{k=1}^{K} \gamma_{m,k} \tilde B_{i, m}(\te, t) B_{k}(t),
\end{align}`
where  `$\tilde B_{i, m}(\te, t) = \sum^Q_{q=1} \tilde\Delta_{i, q} B_{m}(\te)$`.

---
# Simulation - DLNM
- `$\lambda(t|\bfz) = \lambda_0(t)\exp(\int h(t-\te, z(\te))\mathrm{d}\te)$`
- `$t\in (0, 40]$`, `$\te \in [-40, 40]$`, `$z(\te)\in [0, 10]$`

---
# Simulation (2) - TV DLNM
`$\lambda(t|\bfz) = \lambda_0(t)\exp(\int \tilde{h}(t, t-\te, z(\te)) \mathrm {d}\te) = \lambda_0(t)\exp(\int f(t)\cdot h (t-\te, z (\te)) \mathrm{d}\te)$` and
`$f(t) = -\cos(\pi t/t_{\text{max}})$`

---
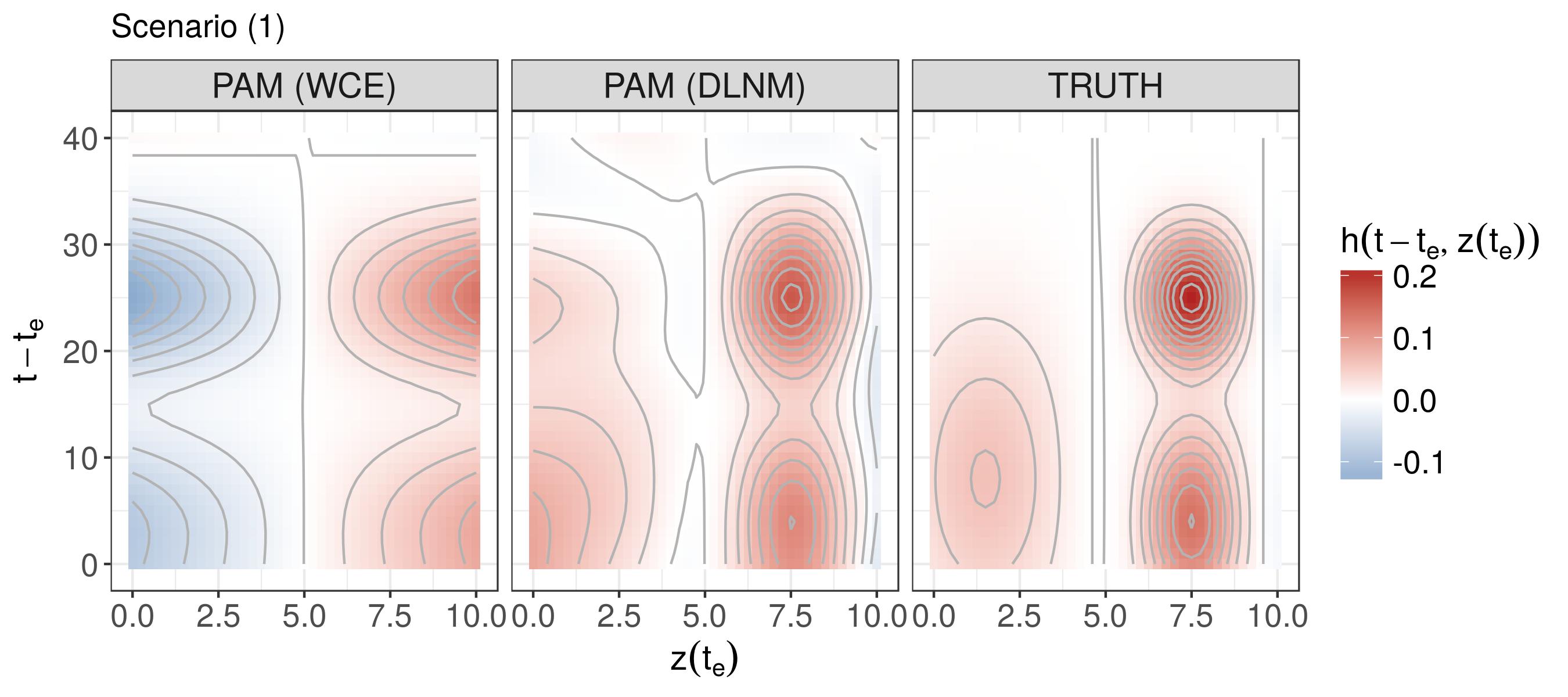
# Application
In the application example ([categorical nutrition](#30)), we estimate
`\begin{align}
  \log\left(\lambda_i(t|\bfx_i, \bfz_i, \ell_i)\right)
    & = f_0(t) +
        \sum_{p=1}^P f_p(x_{i,p}, t) + g(\bfz_i, t) + b_{\ell_i}
\end{align}`
with
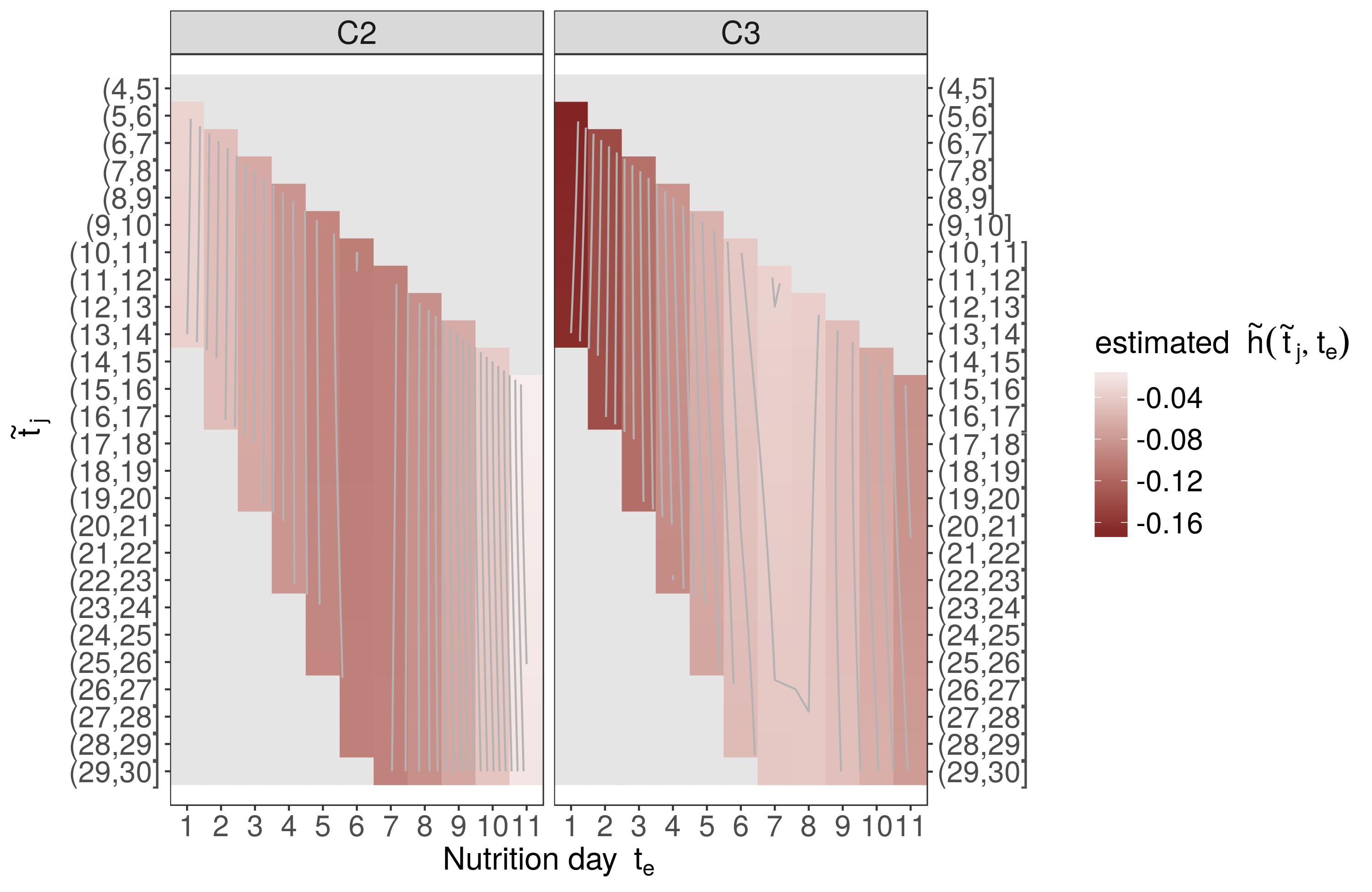
- `$f_{0}(t_j)=\sum_{m=1}^{M}\gamma_{0m}B_m(t_j)$` represents the log baseline-hazard
- `$f(x_{i,p},t_j)=\sum_{m=1}^M\sum_{\ell=1}^{L}\gamma_{m\ell}B_m(x_{i,p})B_\ell (t_j)$` are potentially non-linear, potentially non-linearly time-varying effects
of confounders `$x_{i,p}$`
- `$g(\bfz_i, t) =g_{\CII}(\bfz_i^{\CII},t) + g_{\CIII}(\bfz_i^{\CIII}, t)$`
   - `$\bfz_i^{\CII}$` and `$\bfz_i^{\CIII}$` dummy variables that indicate whether
subject `$i$` received category `$\CII$` and `$\CIII$` nutrition on day
`$t_{e,q},q=1,\ldots,11$`, respectively
  - `$g_{\CII}(\bfz_i,t) \approx \sum^Q_{q=1} \tilde\Delta_{i,q}^{\CII} \tilde h_ {\CII}(t_{e,q}, t)$`
- `$b_{\ell_i}$` is the random effect associated with ICU (cluster) `$\ell_i$`
at which subject `$i$` is treated

`$\ra  \CI$` reference category

---
# PAMM

- We know how the estimate such models in the framework of 
[**G**eneralized **A**dditive **M**ixed **M**odels (**GAMM**s)](https://cran.r-project.org/web/packages/mgcv/index.html)

- Fortunately, we can fit survival models via Poisson GLMs/GAMMs by
representing them as a
[**P**iece-wise exponential **A**dditive **M**ixed **M**odel (**PAMM**s)](https://adibender.github.io/pammtools/)

- to do so requires to
 - divide the follow up `$(0, t_{max}]$` into `$J$` intervals
with `$J+1$` cut-points `$0 = \kappa_0 < \ldots < \kappa_J = t_{\max}$`
 - [transform the data into appropriate format](https://adibender.github.io/pammtools/articles/data-transformation.html) (pseudo observations in
 each interval):
 - interval specific event-indicators `$\delta_{ij}$`, where `$\delta_{ij}=1$`
 if subject `$i$` experienced an event in interval `$j$` (i.e.
 `$t_i\in (\kappa_{j-1}, \kappa_j]$` and `$T_i < C_i$`) and `$\delta_{ij}=0$` else
 - offsets `$o_{ij} = \log(t_{ij})$`, where
 `$t_{ij}=min(t_i - \kappa_{j-1}, \kappa_{j}-\kappa_{j-1})$` is the time
 subject `$i$` spent in interval `$j$`
 - in the `$j^{th}$` interval `$(\kappa_{j-1}, \kappa_j]$` estimate a
 <a href=image/weibull-hazard-ex.jpg> piece-wise constant hazard rate </a>
`$\lambda(t) = \lambda_{j}\ \forall\ t\in (\kappa_{j-1},\kappa_j]$`
(more intervals lead to better approximation)

- See [Holford 1980](http://www.jstor.org/stable/2529982),
[Laird 1981](http://www.jstor.org/stable/2287816),
[Friedman 1982](http://www.jstor.org/stable/2240502),
[Whitehead 1982](http://www.jstor.org/stable/2346901)

---
# Application (Results)

---
# Application (Results)
Example:
- `$\bfz = (5\times \CII, 6\times \CIII)$`
- `$\bfz^{\CII} = (1,1,1,1,1,0,0,0,0,0,0)$`, `$\bfz^{\CIII}=(0,0,0,0,0, 1,1,1,1,1,1)$`
- `$g(\bfz, \tilde{t}_j=18.5) = g(\bfz^{\CII},18.5) + g(\bfz^{\CIII}, 18.5)\approx -0.57$`

`$\ra$` Risk reduction of `$\exp(-0.57)=0.57$` compared to subject with `$11\times\CI$` nutrition (c.p)

---
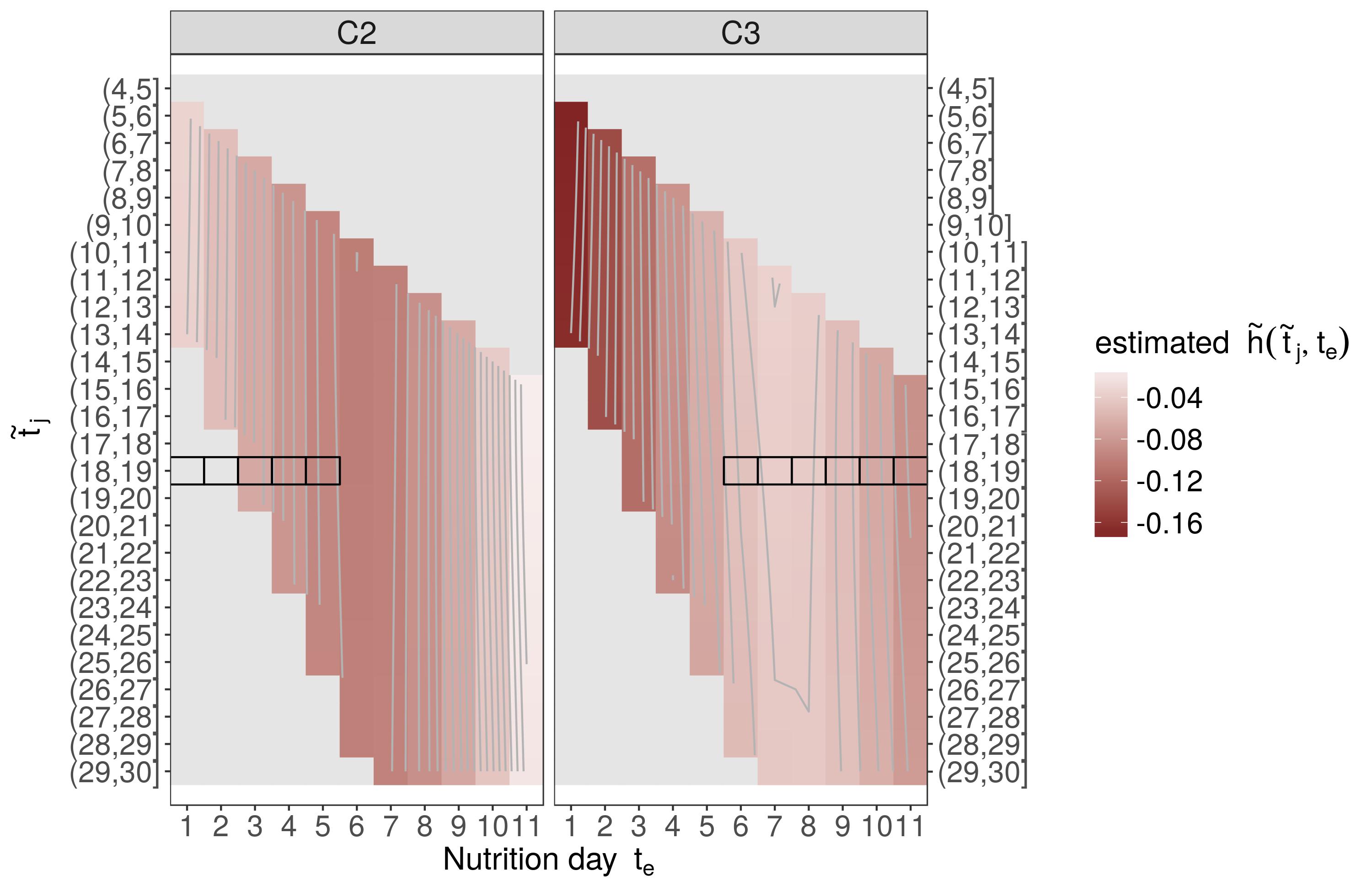
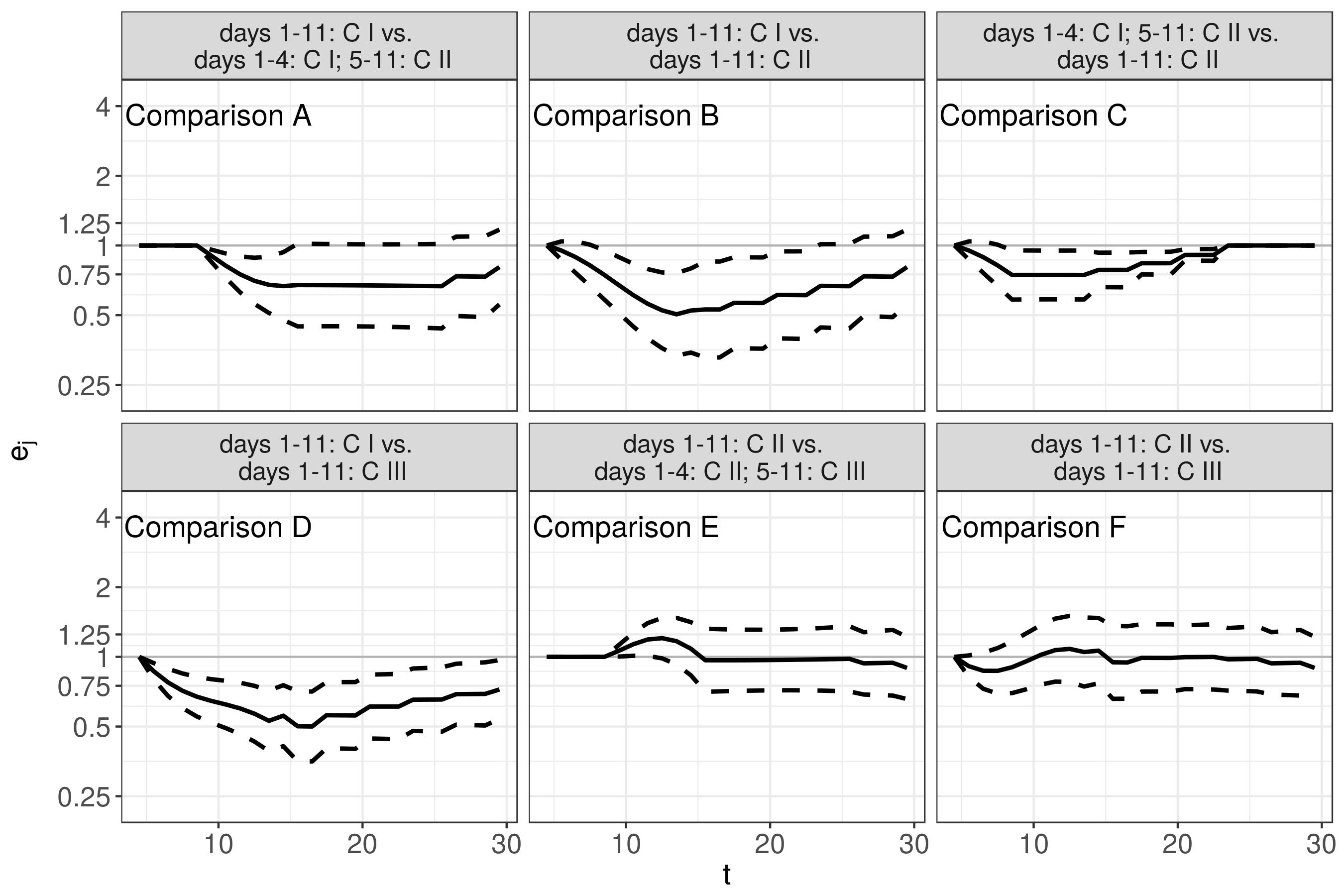
# Application (Results)

These bivariate surfaces are difficult to interpret as

- they must be interpreted with respect to a subject who received
`$\CI$` nutrition on all 11 days of nutrition protocol

- partial effects `$h_{\CII}(t,\te)$` and `$h_{\CIII}(t,\te)$` can both contribute
to the cumulative effect, depending on the specific nutrition profile

- for these reasons, we prefer to analyze and interpret estimated
hazard ratios between hypothetical patients with different clinically
relevant exposure histories ( `$\bfz_1$` and `$\bfz_2$`)

`\begin{equation}
e_j= \frac{\lambda(\tilde t_j|\bfz_2)}{\lambda(\tilde t_j|\bfz_1)}
\end{equation}`

---
# Application (Results)
We compare the following nutrition profiles:

---
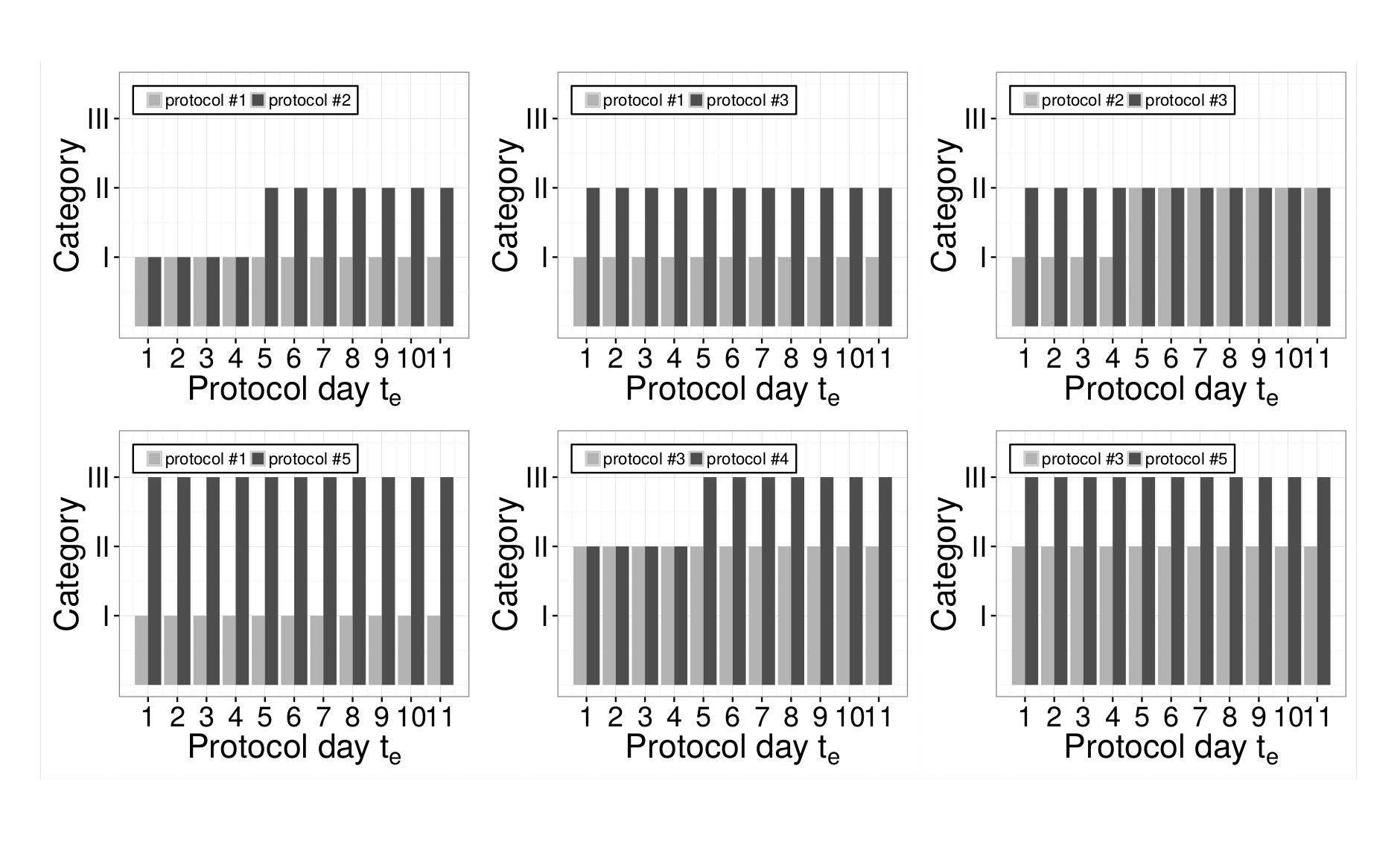
# Application (Results)
`$\ra$` Complete, mildly hypocaloric nutrition reduces risk of mortality
compared to a complete, severely hypocaloric nutrition (Comparison B)

`$\ra$` No further risk reduction when moving from mildly hypocaloric to
partial or complete near target nutrition (Comparisons E, F)

`$\ra$` Sensitivity analyses (Imputation of missing protocols,
lag/lead specification, penalty structure, ...) show no substantive deviation
from main results

---
# Limitations (and outlook)

- currently, `$\tlag$` and `$\tlead$` must be specified a priori
`$\ra$` would be nice if the lag-lead window could be selected data-driven
(e.g. Obermeier et al., 2015)

- we assume that patients released from hospital survived until the end
of the follow-up ( `$t=30$` ). Sensitivity analysis with hospital discharge
as censoring event do not change the results
`$\ra$` Competing risks model for outcomes *hospital discharge* and
*death* would be preferable

- Modeling and interpretation of TDCs always difficult, especially if
exogeneity is unclear, e.g.
  - although nutrition is provided by hospital staff, amount provided might
  depend on patients' health status
  - more recent values provide better confounder adjustment but may also
  be fully indicative of the outcome (indication bias)

- Model choice becomes difficult when all effects are potentially non-linear
and/or non-linearly time-varying (boosting ad double-penalty procedures
promising)

---
# Links and Acknowledgments
- Talk is based on two publications
.font90[
  - Andreas Bender, Andreas Groll, and Fabian Scheipl. 2018. “A Generalized Additive Model Approach to Time-to-Event Analysis.” Statistical Modelling. https://doi.org/10.1177/1471082X17748083.
]
.font90[
  - Andreas Bender, Fabian Scheipl, Wolfgang Hartl, Andrew G Day, Helmut Küchenhoff; "Penalized estimation of complex, non-linear exposure-lag-response associations", Biostatistics, , kxy003, https://doi.org/10.1093/biostatistics/kxy003
]
- [**pammtools**:](https://adibender.github.io/pammtools/) Package for
Piece-wise exponential Additive Mixed Models (in development)[![DOI](https://zenodo.org/badge/106259608.svg)](https://zenodo.org/badge/latestdoi/106259608)

- Slides created via [Yihui Xie](https://twitter.com/xieyihui)'s R package [**xaringan**](https://github.com/yihui/xaringan)
with (modified) [Metropolis theme](https://slides.yihui.name/xaringan/#34)

- All graphics have been created using Hadley Whickham's [ggplot2](http://ggplot2.tidyverse.org/)

- Models are estimated using Simon Wood's [mgcv](https://cran.r-project.org/web/packages/mgcv/index.html)

- Web: [adibender.netlify.com](https://adibender.netlify.com/talk)

- Social:
<a href="https://orcid.org/0000-0001-5628-8611" target="orcid.widget" rel="noopener noreferrer" style="vertical-align:top;"><img src="https://orcid.org/sites/default/files/images/orcid_16x16.png" style="width:1em;margin-right:.5em;" alt="ORCID iD icon"></a>
<a itemprop="sameAs" href ="https://github.com/adibender">
</a>
<a itemprop="sameAs" rel="noopener noreferrer" href="https://www.researchgate.net/profile/Andreas_Bender4" target="_blank"> </a>
<a itemprop="sameAs" href="//twitter.com/adiBender" target="_blank">
 </a>

---
# References
- Friedman, Michael. “Piecewise Exponential Models for Survival Data with Covariates.” The Annals of Statistics 10, no. 1 (1982): 101–113.
- Gasparrini, Antonio. “Modeling Exposure–lag–response Associations with Distributed Lag Non-Linear Models.” Statistics in Medicine 33, no. 5 (February 28, 2014): 881–99. https://doi.org/10.1002/sim.5963.
- Gasparrini, Antonio, Fabian Scheipl, Ben Armstrong, and Michael G. Kenward. “A Penalized Framework for Distributed Lag Non-Linear Models.” Biometrics, January 1, 2017. https://doi.org/10.1111/biom.12645.
- Holford, Theodore R. “The Analysis of Rates and of Survivorship Using
Log-Linear Models.” Biometrics 36, no. 2 (1980): 299–305. https://doi.org/10.2307/2529982.
- Laird, Nan, and Donald Olivier. “Covariance Analysis of Censored Survival Data
Using Log-Linear Analysis Techniques.” Journal of the American Statistical Association 76, no. 374 (1981): 231–240. https://doi.org/10.2307/2287816.
- Marra, Giampiero, and Simon N. Wood. “Coverage Properties of Confidence
Intervals for Generalized Additive Model Components.” Scandinavian Journal of Statistics 39, no. 1 (March 1, 2012): 53–74. https://doi.org/10.1111/j.1467-9469.2011.00760.x.
- Sylvestre, Marie-Pierre, and Michal Abrahamowicz. “Flexible Modeling of the Cumulative Effects of Time-Dependent Exposures on the Hazard.” Statistics in Medicine 28, no. 27 (2009): 3437–3453. https://doi.org/10.1002/sim.3701.

---
# References
- Whitehead, John. “Fitting Cox’s Regression Model to Survival Data Using GLIM.” Journal of the Royal Statistical Society. Series C (Applied Statistics) 29, no. 3 (1980): 268–75. https://doi.org/10.2307/2346901.
- Wood, Simon N. Generalized Additive Models: An Introduction with R. Boca Raton and FL: Chapman & Hall/CRC, 2006.
- Wood, Simon N. “Low-Rank Scale-Invariant Tensor Product Smooths for
Generalized Additive Mixed Models.” Biometrics 62, no. 4 (December 1, 2006): 1025–36. https://doi.org/10.1111/j.1541-0420.2006.00574.x.
- Wood, Simon N. “Fast Stable Restricted Maximum Likelihood and Marginal
Likelihood Estimation of Semiparametric Generalized Linear Models.”
Journal of the Royal Statistical Society: Series B (Statistical Methodology) 73, no. 1 (2011): 3–36. https://doi.org/10.1111/j.1467-9868.2010.00749.x.
- Wood, Simon N. “On P-Values for Smooth Components of an Extended Generalized Additive Model.” Biometrika 100, no. 1 (March 1, 2013): 221–28. https://doi.org/10.1093/biomet/ass048.
- Wood, Simon N., Fabian Scheipl, and Julian J. Faraway. “Straightforward Intermediate Rank Tensor Product Smoothing in Mixed Models.” Statistics and Computing, 2012. https://doi.org/10.1007/s11222-012-9314-z.

---
# References
- Wickham, Hadley. Ggplot2: Elegant Graphics for Data Analysis. 2nd ed. 2016. New York, NY: Springer, 2016.
- Yihui Xie (2017). xaringan: Presentation Ninja. R package version
  0.4.4. https://github.com/yihui/xaringan
- Hadley Wickham, Romain Francois, Lionel Henry and Kirill Müller
  (2017). dplyr: A Grammar of Data Manipulation. R package version
  0.7.4. https://CRAN.R-project.org/package=dplyr

---
# Caloric Adequacy

- **caloric intake** = calories from EN + PN + PF

- **caloric adequacy (CA)**: 
`$CA (\%) = \text{caloric intake} / \text{prescribed calories} \cdot 100$`

- **discretized caloric adequacy (in 3 categories)**:
 - `$\CI$`: `$0\% \leq CA < 30\%$` and no OI
 - `$\CII$`:
 - `$30\% \leq CA < 70\%$` and no OI *or*
 - `$0\% \leq CA < 30\%$` and additional OI
 - `$\CIII$`:
 - `$CA \geq 70\%$` *or*
 - `$30\% \leq CA < 70\%$` and additional OI