+ - 0:00:00
Notes for current slide
Notes for next slide

\usepackageamsmath,amssymb,bm

pammtools
Survival Analysis with Generalized Additive Mixed Models

R Medicine 2020




Andreas Bender (@adibender),
Fabian Scheipl, Philipp Kopper




Department of Statistics, LMU Munich

1

@adibender                            

Time-to-event Analysis (Survival Analysis) requires special methods because

  • outcome can not always be fully observed (censoring, truncation)

  • covariate values can change over time (time-varying covariates)

  • covariate effects can change over time (time-varying effects)

  • competing events prevent observation of the event of interest (competing risks)

  • observation units transition between different states (recurrent events, multi-state models)

2

\usepackageamsmath,amssymb,bm

@adibender                            

Hitorically Survival Analysis dominated by Cox type models

Many Survival Models can be represented as Poisson Regression (on transformed data)

3

\usepackageamsmath,amssymb,bm

@adibender                            

Hitorically Survival Analysis dominated by Cox type models

Many Survival Models can be represented as Poisson Regression (on transformed data)

→ Use any method/R package for Survival Analysis that supports optimization of Poisson Likelihood (e.g., GAMMs via mgcv; Wood (2017))

3

\usepackageamsmath,amssymb,bm

@adibender                            

4

\usepackageamsmath,amssymb,bm

Survival Analysis as Poisson Regression

5

@adibender                            
Data in "standard" time-to-event format
Data in PED format


→ transform to PED using intervals cut points 0,1,1.5 and 3

6

@adibender                            
Data in "standard" time-to-event format
Data in PED format


→ transform to PED using intervals cut points 0,1,1.5 and 3

6

@adibender                            
Data in "standard" time-to-event format
Data in PED format


→ transform to PED using intervals cut points 0,1,1.5 and 3

6

@adibender                            
Data in "standard" time-to-event format
Data in PED format


→ transform to PED using intervals cut points 0,1,1.5 and 3

6

@adibender                            
Data in "standard" time-to-event format
Data in PED format


→ transform to PED using intervals cut points 0,1,1.5 and 3

6

The pammtools package

7

@adibender                            

pammtools facilitates

  • data transformation (as_ped):

    • right-censoring
    • competing risks

  • post-processing:

    • prediction (add_hazard, add_surv_prob, add_cif),
    • model evaluation (integrated brier score via pec)

  • convenience functions

8

@adibender                            
library(pammtools)
data("tumor")
days status age sex complications
311 1 65 male no
469 0 82 female no
1257 1 66 female no
1 1 96 female yes
13 1 72 male yes
1542 0 29 male yes
9

@adibender                            

Data Transformation

ped <- tumor %>% as_ped(Surv(days, status) ~ .)
id tstart tend interval offset ped_status age sex complications
167 0 1 (0,1] 0.0000000 0 64 male yes
167 1 2 (1,2] 0.0000000 0 64 male yes
167 2 3 (2,3] 0.0000000 0 64 male yes
167 3 5 (3,5] 0.6931472 0 64 male yes
167 5 6 (5,6] 0.0000000 0 64 male yes
167 6 7 (6,7] 0.0000000 0 64 male yes
167 7 8 (7,8] 0.0000000 1 64 male yes
397 0 1 (0,1] 0.0000000 0 68 female yes
397 1 2 (1,2] 0.0000000 0 68 female yes
397 2 3 (2,3] 0.0000000 1 68 female yes
10

@adibender                            

Propportional Hazards Model

pam1 <- mgcv::gam(
  formula = ped_status ~ s(tend) + sex + complications + s(age),
  data    = ped,
  family  = poisson(),
  offset  = offset)
summary(pam1)
## Parametric coefficients:
##                  Estimate Std. Error z value Pr(>|z|)
## (Intercept)      -7.86165    0.08396 -93.632  < 2e-16 ***
## sexfemale         0.12095    0.10604   1.141    0.254
## complicationsyes  0.68619    0.10695   6.416  1.4e-10 ***
## Approximate significance of smooth terms:
##           edf Ref.df Chi.sq  p-value
## s(tend) 3.794  4.717  19.83  0.00116 **
## s(age)  4.903  5.920  28.56 8.04e-05 ***
...
11

@adibender                            

Hazard

hazard_df <- ped %>%
  make_newdata(tend = unique(tend), complications = unique(complications)) %>%
  add_hazard(pam1) # age fixed at mean, sex at modus value
interval tend complications hazard ci_lower ci_upper
(0,1] 1 no 0.0005227 0.0003787 0.0007215
(1,2] 2 no 0.0005219 0.0003783 0.0007198
(2,3] 3 no 0.0005210 0.0003780 0.0007181
(0,1] 1 yes 0.0010381 0.0007420 0.0014524
(1,2] 2 yes 0.0010365 0.0007414 0.0014491
(2,3] 3 yes 0.0010348 0.0007407 0.0014458
12

@adibender                            

Survival Porbability

surv_prob <- ped %>%
  make_newdata(tend = unique(tend), complications = unique(complications)) %>%
  group_by(complications) %>% # important !!
  add_surv_prob(pam1)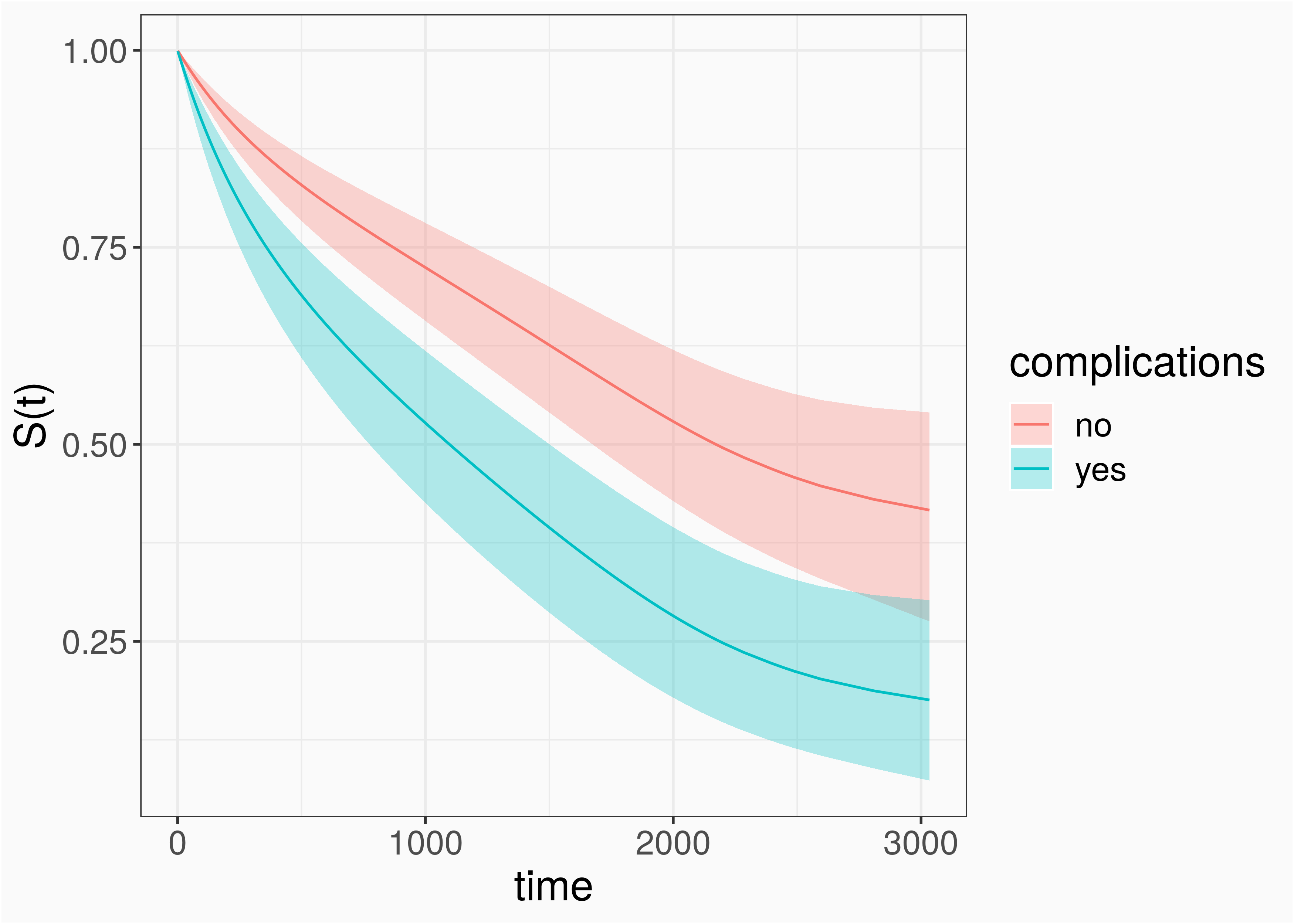

13

@adibender                            

Stratified Model

pam2 <- pamm(
  formula = ped_status ~ s(tend, by = complications) + sex + s(age),
  data    = ped)
summary(pam2)
## Parametric coefficients:
##             Estimate Std. Error z value Pr(>|z|)
## (Intercept) -7.78558    0.07921 -98.288   <2e-16 ***
## sexfemale    0.15409    0.10584   1.456    0.145
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Approximate significance of smooth terms:
##                            edf Ref.df  Chi.sq p-value
## s(tend):complicationsno  6.102  7.279   8.717   0.293
## s(tend):complicationsyes 6.096  7.224 126.152 < 2e-16 ***
## s(age)                   1.051  1.101  23.819 1.6e-06 ***
...
14

@adibender                            

Stratified Model (Hazard)

gg_slice(ped, pam2, term = "tend",
  tend = seq(0,1000, by = 10), complications = unique(complications))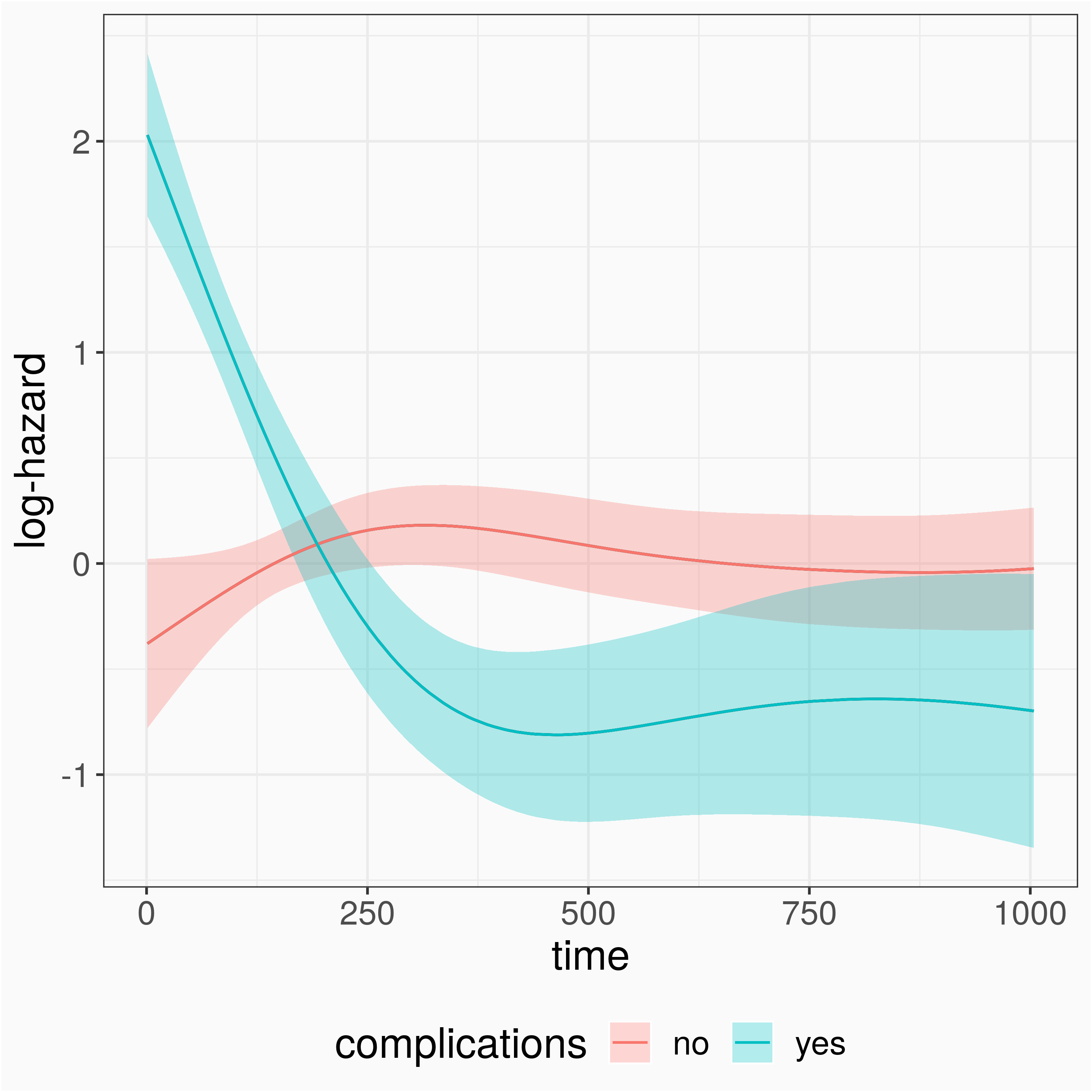

15

@adibender                            
16

References

Bender, A. et al. (2018). "A generalized additive model approach to time-to-event analysis". En. In: Statistical Modelling 18.3-4, pp. 299-321. ISSN: 1471-082X. DOI: 10.1177/1471082X17748083.

Bender, A. et al. (2020). "A General Machine Learning Framework for Survival Analysis". In: arXiv:2006.15442 [cs, stat]. arXiv: 2006.15442.

Cai, T. et al. (2002). "Mixed Model-Based Hazard Estimation". In: Journal of Computational and Graphical Statistics 11.4, pp. 784-798. ISSN: 1061-8600. DOI: 10.1198/106186002862. URL: http://dx.doi.org/10.1198/106186002862 (visited on Jan. 07, 2015).

Friedman, M. (1982). "Piecewise Exponential Models for Survival Data with Covariates". In: The Annals of Statistics 10.1, pp. 101-113. ISSN: 00905364. URL: http://www.jstor.org/stable/2240502.

Laird, N. et al. (1981). "Covariance Analysis of Censored Survival Data Using Log-Linear Analysis Techniques". In: Journal of the American Statistical Association 76.374, pp. 231-240. DOI: 10.2307/2287816. URL: http://www.jstor.org/stable/2287816.

Wood, S. N. (2017). Generalized Additive Models: An Introduction with R. Englisch. 2 Rev ed.. Boca Raton: Chapman & Hall/Crc Texts in Statistical Science. ISBN: 978-1-4987-2833-1.

17

@adibender                            

Time-to-event Analysis (Survival Analysis) requires special methods because

  • outcome can not always be fully observed (censoring, truncation)

  • covariate values can change over time (time-varying covariates)

  • covariate effects can change over time (time-varying effects)

  • competing events prevent observation of the event of interest (competing risks)

  • observation units transition between different states (recurrent events, multi-state models)

2

\usepackageamsmath,amssymb,bm

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow